The DO Loop
Statistical programming in SAS with an emphasis on SAS/IML programs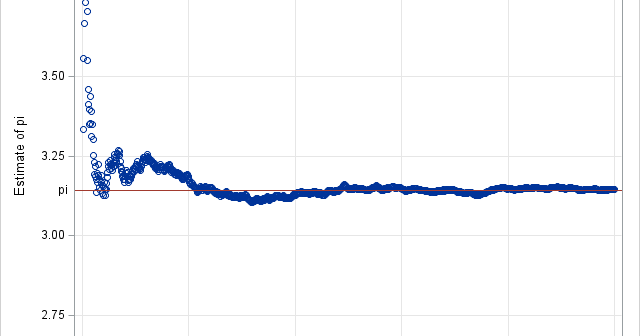
Welcome to Pi Day 2026! Every year on March 14th (written 3/14 in the US), people in the mathematical sciences celebrate "all things pi-related" because 3.14 is the three-decimal approximation to π ≈ 3.14159265358979.... The purpose of this day is to have fun and celebrate the importance and ubiquity of
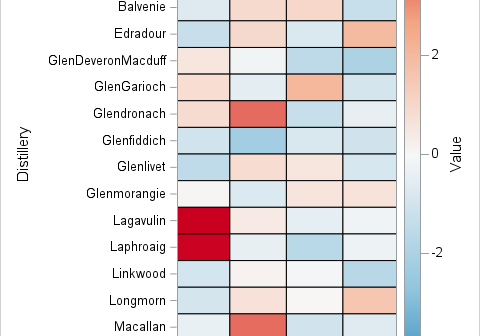
SAS procedures automatically generate many graphs when you turn on ODS graphics. For example, I have written about how to interpret the graphs that are produced automatically when you use PROC PRINCOMP to perform a principal component analysis (PCA). The built-in graphs are well-designed and informative, but this article discusses
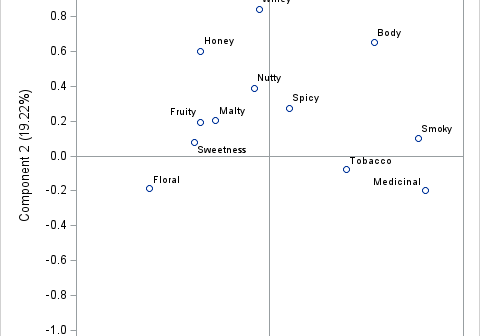
Good old Scotch drink! Inspire me, until I lisp and wink, To sing your name! -- Robert Burns (1785) Scotch whisky (spelled without an 'e') is a popular drink that makes up a multi-billion dollar industry. Scotch whisky accounts for almost 75% of Scotland's food and drink exports! Poets
